Auto-Encoder
Here is a typical notation for an autoencoder.
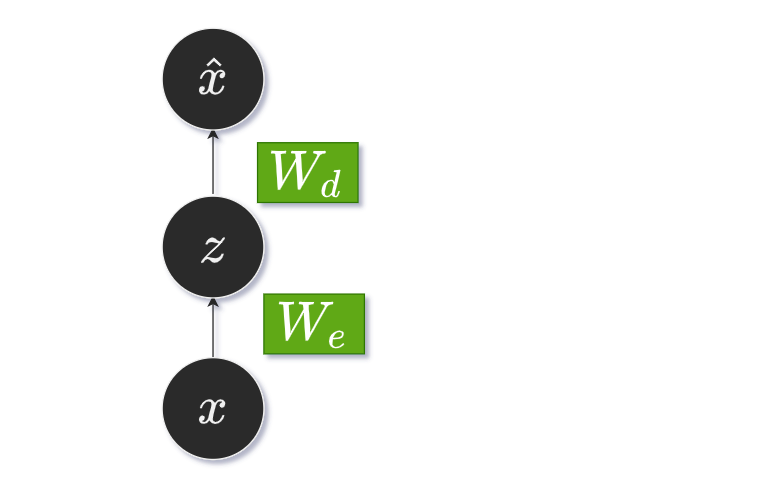
This would be the input $\boldsymbol x \in \mathbb R^n$, the latent state $\boldsymbol z \in \mathbb R^d$, where $d$ is the dimension of the latent space, which may be $d \lt n$, but it may also be $d \ge n$.
Finally the $\boldsymbol {\hat x} \in \mathbb R^n$, again the same dimension of the input.
We can write two equations here:
\[\boldsymbol z=f(W_e \boldsymbol x + b_e) \\ \boldsymbol {\hat x}=f(W_d \boldsymbol z + b_d)\]where $f$ is some nonlinearity (activation function). The dimensions of the matrices:
- $W_e \in \mathbb R^{d \times n}$ is the encoder matrix
- $W_d \in \mathbb R^{n \times d}$ is the decoder matrix
The very special case for the autoencoder is $W_e = W_d^T,$ when the matrices are transposed.
Loss functions
When $m$ is the number of samples, and $\ell(\boldsymbol{x}^{(j)}, \boldsymbol{ \hat x}^{(j)} )$ is per sample loss we can express the loss as an average of per sample losses:
\[\mathcal{L}=\frac{1}{m} \sum_{j=1}^{m} \ell\left(\boldsymbol{x}^{(j)}, \boldsymbol{\hat{x}}^{(j)}\right)\]There are two frequent cases:
- when $x_{i} \in {0,1}$ we can use binary cross entropy loss where the outputs $\hat x$ will be in between 0 and 1 thanks to sigmoid function:
- when $x_i \in \mathbb R$ we can use MSE for instance:
The idea of the manifold
The idea of manifold is based on observation that images of something, e.g. facial expressions define a smooth manifold in the high dimensional image space (space of all the images).
If we somehow find this manifold we could move through it and we would experience all the facial expressions.
This manifold is then highly connected with the facial degrees of freedom (head muscles movements).
Here is a more complex definition of manifold.
Types of autoencoders
- Denoising autoencoder
- Sparse Autoencoder
- Deep Autoencoder
- Contractive Autoencoder
- Undercomplete Autoencoder
- Convolutional Autoencoder
- Variational Autoencoder
Denoising autoencoder
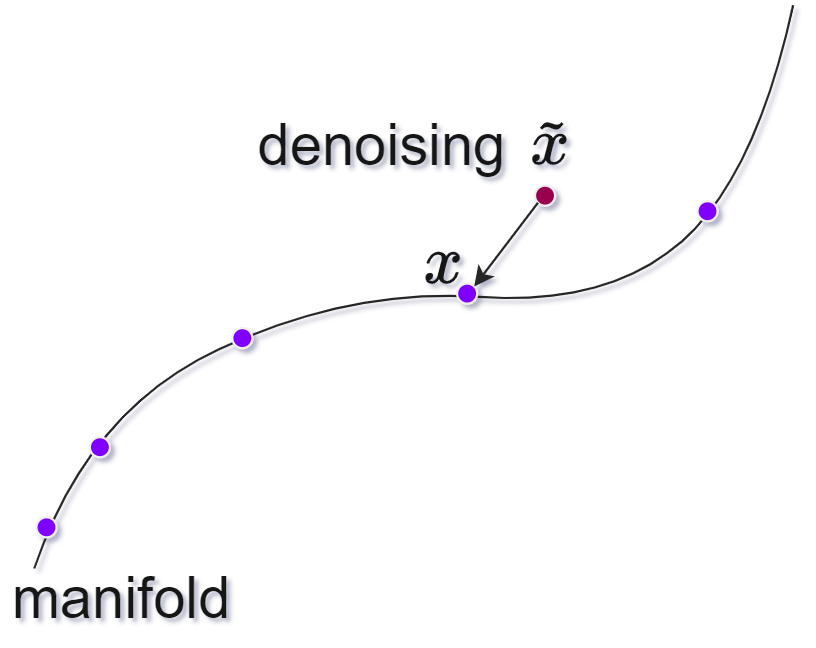
In here $x$ is an image without the noise and $\tilde x$ image with noise.
Typically denoising autoencoders are trained on a specific image set, say faces, and once trained we experiment with noisy image faces, and they should be denoised.
Sparse Autoencoder
A sparse autoencoder has sparsity penalty. Sparsity penalty means altered loss function that penalizes activations of hidden layers and only few nodes are activated per sample input.
The intuition: if a student claims to be an expert in several areas he might be just learning some quite shallow knowledge. However, if a student claims to know just one area well we should find he is an expert even if we provide him problems with missing details (fewer nodes activation).
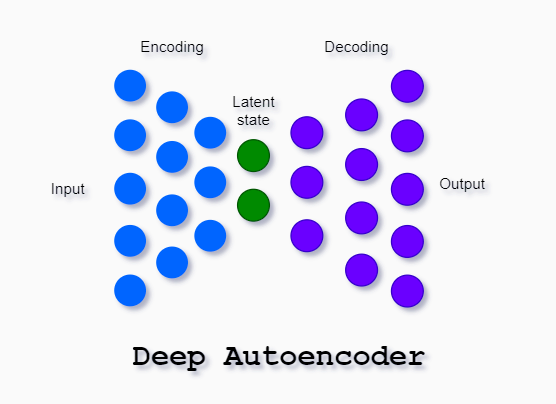
Deep Autoencoder
Deep autoencoder is two symmetrical networks each having several (e.g. three) shallow layers representing encoding and decoding parts of the net.
Contractive Autoencoder
A Contractive Autoencoder adds a specific penalty term to the loss function. Penalty is a Frobenius norm of the Jacobian matrix of the encoder activations with respect to the input.
The penalty impact is lower-dimensional non-linear manifold, being more invariant to the vast majority of directions orthogonal to the manifold.
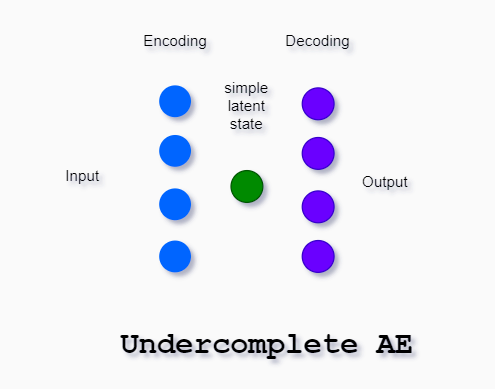
Undercomplete Autoencoder
If we constrain the number of nodes present in the hidden layer of the network we limit the amount of information that can flow through the network.
This way the model can learn the most important attributes of the input data.
Convolutional Autoencoder
A convolutional autoencoder encoder is ConvNet that produces a low-dimensional representation of the image. The decoder, also ConvNet, will reconstruct the original image.
Convolutional AE can be used for image coloring or noise reduction.
Variational autoencoder
I believe this type of autoencoder is the new GAN. It deserves a separate VAE article.