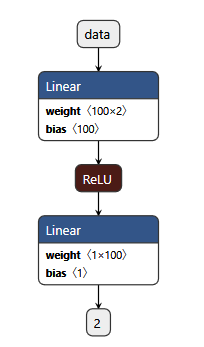
Learning the sum operation (regression)

Typical regression problem would be to learn the sum (+) operation with this neural net:

Although this is fairly easy problem, it is very important to provide some tips on regression, and the advantages over the classification for this particular case.

If you would set neural net for the sum operation as a classification problem, you would solve the limited amount of experiments, those you have trained.

With regression, this is not the case. Regression can solve with some error margin any problem close to the original training data distribution.

Here is the demo.

As you may understand from the demo training was on a very limited set of examples:

(0.2000, 0.0000) -> 0.2000
(0.4000, 0.5000) -> 0.9000
(0.0000, 0.5000) -> 0.5000

where the first tuple (numbers we add) were from the list:

[0.0, 0.1, 0.2, 0.3, 0.4].

At the end we were able to get very accurate result using the addends not present in the training set, say: 0.1200 + 0.4100 = 0.5295.

In here the sum 0.5295 was never part of the training set.

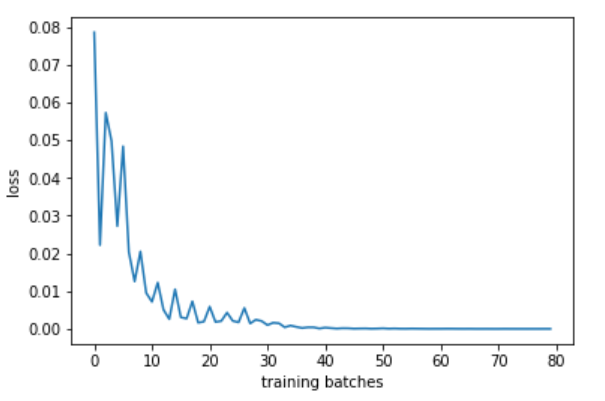
The next image shows how the training loss decreased over the time when training our batches:

Even with the data outside of the original input distribution, like in case 0.3000 + 0.7000 = 0.9793 we got pretty accurate result.

This all shows regression can be used as an interpolation (approximation) technique in some cases.