LAMB

LAMB (Layer-wise Adaptive Moments optimizer for Batch training) is another optimizer algorithm for the first time presented in this paper.

They claimed to train the BERT model for 76 minutes, which is excellent knowing that the previous results took over a day on the same architecture.

This is achieved by increasing the batch size to the memory limit of a GPU (TPU), and introducing the “pomero” function.

Let’s dig into it.

LAMB is based on Adam so you may check my previous article on Adam first.

Like in Adam algorithm we use gradients $grad_t$ and gradients squared $grad_t^2$ and we calculate the average grad $m_t$ and average gradient squared $v_t$ thanks to the EWMA (exponentially weighted moving average) formula and debiasing.

In LAMB we also use the pomero function.

    def pomero(t):
        '''power 2, mean, square root = pomero'''
        return t.pow(2).mean().sqrt()

Here t is our parameter tensor where we square each tensor value at any index, take the mean and then the square root of that mean.

Let’s explain what pomero will do in a diagram:

t = torch.randn(22)
q = t.pow(2)
m = q.mean()
r = m.sqrt()
plt.scatter(range(0,22), t) #blue
plt.scatter(range(0,22), q) #orange
plt.scatter(range(0,1), m) #green
plt.scatter(range(1,2), r) #red

p = pomero(t)
plt.scatter(range(2,3), p) #violet

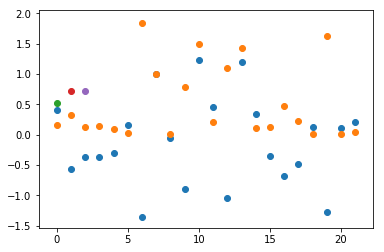
Blue dot’s are data from the normal distribution, orange dots are squares of blues, green dots are the mean of oranges, and the red and violet dots are the same pomero.

We created and named the function pomero to express the power, mean and square root, operation.

Inside LAMB at the very end we will calculate the two “pomeros” pom1 and pom2.

pom1 = pomero(p.data)
pom2 = pomero(step)

Where p.data is the parameter, and the step is the Adam step. Note we removed the weight decay entirely because it is not needed. We will use batch norms anyway.

Then the final update of param p would be

p.data = p.data - lr*pom1/pom2 * step

Or to express this in simple words we take the old param and add the gradient descent. In here lr*pom1/pom2 is constant value for each bach and step is a tensor with the same dimension as the first order gradient.

Again step is the debiased gradient momentum in the numerator, and in the denominator it is square root of the debiased gradient squared momentum.

Here is the simplified LAMB code in PyTorch.

class Lamb(Optimizer):

    def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8):
        
        defaults = dict(lr=lr, betas=betas, eps=eps)
        super(Lamb, self).__init__(params, defaults)

    def __setstate__(self, state):
        super(Lamb, self).__setstate__(state)

    def pomero(self,t):        
        return t.pow(2).mean().sqrt()
    
    def step(self, closure=None):        
        
        for group in self.param_groups:
            for p in group['params']:
                
                if p.grad is None:
                    continue  
                    
                grad = p.grad.data                
                state = self.state[p] 
                
                if len(state) == 0:
                    state['step'] = 0                    
                    state['agrad'] = torch.zeros_like(p.data) # grad average
                    state['agrad2'] = torch.zeros_like(p.data) # Hadamar grad average
                    
                state['step'] += 1
                
                agrad, agrad2 = state['agrad'], state['agrad2'] 
                beta1, beta2 = group['betas']
                
                agrad.mul_(beta1).add_(1 - beta1, grad)
                agrad2.mul_(beta2).addcmul_(1 - beta2, grad, grad) 

                bias_1 = 1 - beta1 ** state['step']
                bias_2 = 1 - beta2 ** state['step'] 
                
                agrad = agrad.div(bias_1)
                agrad2 = agrad2.div(bias_2)
                
                step = agrad / agrad2.sqrt().add_(group['eps'])
                pom1 = self.pomero(p.data)
                pom2 = self.pomero(step)
            
                p.data.add_(-group['lr']*pom1/pom2, step)

        return loss