Convolution details in PyTorch
1D Convolution
This would be the 1d convolution in PyTorch
import torch
import torch.nn.functional as F
# batch, in, iW (input width)
inputs = torch.randn(2, 1, 2)
# out, in, kW (kernel width)
filters = torch.randn(1, 1, 2)
print("\ninputs:", inputs)
print("\nfilters:", filters)
res = F.conv1d(inputs, filters, padding=0)
print("\nsize:", res.size())
print(res)
Out:
inputs: tensor([[[-1.3681, 0.8410]],
[[-1.1009, 0.0678]]])
filters: tensor([[[1.5199, 0.8276]]])
size: torch.Size([2, 1, 1])
tensor([[[-1.3833]],
[[-1.6172]]])
This is the output worth interpreting.
At first we need to provide the input and the kernel to convolve.
Input should have the format starting with minibatch size, followed by input size and then followed by input width iW.
The single dimension of input means the input will have just the width. The line:
inputs = torch.randn(2, 1, 2) means minibatch size is two, input size is just 1 and the input width is just 2.
The filters tensor should have rank 3 for conv1d. Again we need to provide the output size, the input size and the kernel width. The constraint is the kernel width kW must always be equal or less than input width iW.
2D Convolution
# 2D convolution example
import torch.nn.functional as F
from matplotlib import pyplot as plt
img = x_train[0]/255
img.resize_(28,28)
print("img show:", img.size())
plt.imshow(img, cmap="gray")
plt.show()
k = torch.tensor([1.,1.,1., 0.,0.,0., -1.,-1.,-1.]).reshape(3,3).unsqueeze(0).unsqueeze(0)
print("kernel:", k.size())
# see how the dimensions of img and k should match
img2 = img.unsqueeze(0).unsqueeze(0)
print("img before conv2d:", img2.size())
res=F.conv2d(img2, k, padding=1)
print(res.size())
rest = res.squeeze()
plt.imshow(rest, cmap="gray")
plt.show()
Out:
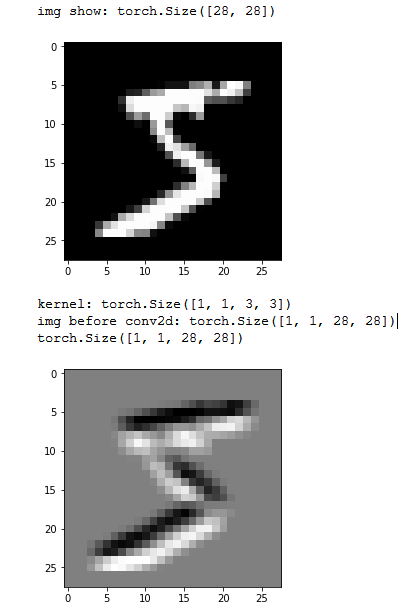
As you may understand from the image, the purpose of the convolution is to extract certain image features.
Input image size was 1,1,28,28 and the meaning of these numbers are the mini batch size, in channels, input width iW, input height iH.
Then we have the kernel of size 1,1,3,3, and in here the meaning of these numbers is similar as for the conv1d.
First one means the out size, then the in size, then the kW and kH.
Again the same rule must be, the kernel size must be smaller or equal to the input size. Since I used a little bit of padding I got the same output shape of 28x28.
Note that in the later example I used the convolution kernel that will sum to 0.
Convolution to linear
It is not easy to understand the how we ended from
self.conv2 = nn.Conv2d(20, 50, 5) to self.fc1 = nn.Linear(4*4*50, 500) in the next example.
class M(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 20, 5)
self.conv2 = nn.Conv2d(20, 50, 5)
self.fc1 = nn.Linear(4*4*50, 500)
self.fc2 = nn.Linear(500, 10)
def forward(self, x):
x = x.view(-1, 1, 28, 28)
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
Common sense is telling us that in and out should follow the same pattern all over again. E.g. self.conv1 has in=1 and out=20.
self.conv2 takes the out from the previous layer as in=20 and outputs out=50.
self.fc2 takes the in=500 which is the out from slef.fc1
fc* means fully connected
But it is not like that. The next two lines break this seemingly obvious pattern.
self.conv2 = nn.Conv2d(20, 50, 5)
self.fc1 = nn.Linear(4*4*50, 500)
In fact this pattern does work for linear layers, but may not work for convolution layers.
To understand, we should print x size after every line.
The next code also has the comments explaining the dimensions.
def forward(self, x):
print(x.size()) #torch.Size([64, 784])
x = x.view(-1, 1, 28, 28)
print(x.size()) #torch.Size([64, 1, 28, 28])
x = F.relu(self.conv1(x))
print(x.size()) #torch.Size([64, 20, 24, 24])
x = F.max_pool2d(x, 2)
print(x.size()) #torch.Size([64, 20, 12, 12])
x = F.relu(self.conv2(x))
print(x.size()) #torch.Size([64, 50, 8, 8])
x = F.max_pool2d(x, 2)
print(x.size()) #torch.Size([64, 50, 4, 4])
x = x.view(x.size(0), -1)
print(x.size()) #torch.Size([64, 800])
x = F.relu(self.fc1(x))
print(x.size()) #torch.Size([64, 500])
x = self.fc2(x)
print(x.size()) #torch.Size([64, 10])
return x
As we can see before we enter the self.fc1 we end in the size torch.Size([64, 50, 4, 4]) that depends on the input size.
How do we get the convolution filters?
w = model.conv1.weight
b = model.conv1.bias
Why do we need max pooling?
It is great for detecting the edges, since max operation forces it to pick up the edge values. It is also great for isolating the image details. Searching for hands in the image for example.
Can we compare nn.Conv2d first two parameters with nn.Linear first two parameters?
nn.Linear creates a matrix of NxM. If we ignore the bias parameters we have NxM parameters.
For nn.Conv2d to calculate the parameters it is little funky, since it depends on kernel size:
c = nn.Conv2d(5,10, 2,2)
for _ in c.parameters():
print(_.size())
print(_.nelement())
# torch.Size([10, 5, 2, 2])
# 200
# torch.Size([10]) ==> bias
# 10
So generally we cannot compare these two.
Are the nn.Conv2d parameters the filters?
Yes, weight parameters represent the filters.
Are Conv2d kernels equivalent to conv memory?
Yes, since we learned that with GD.
What is nn.Linear FC layer memory?
The parameters of nn.Linear layer, weights and bias represent the memory.
Is convolution with stride 2 equivalent to the convolution with stride 1 and the max pooling layer of 2?
No it is not. The following example explains the output is completely different, but the dimension of the output is the same.
tt = torch.randn(1,1,6,6)
# 3x3 convolution kernel
kk = torch.randn(1,1,3,3)
# assumption convolution with stride 2 is equal as conv with stride 1 and max pooling of 2
res1 = F.conv2d(tt, kk, stride=2)
print(res1)
# tensor([[[[ 2.1621, 7.2672], [-1.5460, -1.2396]]]])
res2 = F.conv2d(tt, kk, stride=1)
res2 = F.max_pool2d(res2,2)
print(res2)
# tensor([[[[5.8472, 7.2672], [1.3216, 1.9220]]]])
Should we use bias in conv2d?
It is possible to use bias, but often it is ignored, by setting it with bias=False. This is because we usually use the BN behind the conv layer which has bias itself.
nn.Conv2d(1, 20, 5, bias=False)
Why do we have max pooling to lower the resolution and at the same time we increase the number of filters?
By increasing the number of filters and by lowering the image using max pooling we try to keep the same number of features.
What nn.Conv2d(3,10, 2,2) numbers 3 and 10?
The in_channels in the beginning is 3 for images with 3 channels (colored images). For images black and white it should be 1. Some satellite images may have 4 in there.
The out_channels is the number of convolution filters we have: 10. The filters will be of size 2x2.
What is dilation?
To explain what dilation is you can simple understand from these two images:


Why a 3x3 filter is the best.
According to the paper from Max Zeiler. 17.3.3346
Few more tips about convolution
- Convolution is
positiontranslation invariant and handles location, but not actions. - In PyTorch convolution is actually implemented as correlation.
- In PyTorch
nn.ConvNdandF.convNddo have reverse order of parameters.
Bag of tricks for CONV networks
This Bag of tricks paper presents many tricks to be used for Convolutional Neural Networks such as:
- Large batch training
- Low precision training
- Decay of the learning rate
- Resnet tweaks
- Label smoothing
- Mixup training
- Transfer learning
- Semantic segmentation