Backpropagation honorable notes
Backpropagation is a very popular neural network learning algorithm because it is conceptually simple, computationally efficient, and because it often works.
Here we will calculate derivative using backprop in a point p=(5,3,2). We will simple implement backprop in a point without using the chain rule.
Notice how we defined a function y=3*(a + b*c) and how we use e=0.01 to calculate the derivative.
a=5
b=3
c=2
def f(a,b,c):
return 3*(a + b*c)
y= f(a,b,c)
print(y)
e =0.01 #some small number
'''gradients da,db,dc'''
da = (f(a+e,b,c)-f(a,b,c))/e
print(da)
db = (f(a,b+e,c)-f(a,b,c))/e
print(db)
dc = (f(a,b,c+e)-f(a,b,c))/e
print(dc)
The output would be like this:
33
3.0000000000001137
6.000000000000227
8.99999999999963
To understand this, the first printed value 33 is the y at a point p=(5,3,2).
The derivative of a function y = f(a,b,c) of a variable a is a measure of the rate at which the value y of the function changes with respect to the change of the variable a. It is called the “derivative of f with respect to x”.
In here we used calculus to effectively get the values da, db and dc.
When this calculus may fail?
Consider this example:
import numpy as np
import matplotlib.pyplot as plt
def f(x): #sigmoid
return 1 / (1 + np.exp(-x))
# create 100 equally spaced points between -10 and 10
x = np.linspace(-10, 10, 100)
# calculate the y value for each element of the x vector
y = f(x)
fig, ax = plt.subplots()
ax.plot(x, y)
plt.show()
e = 0.001
x=1
dx = (f(x+e)-f(x))/e
print("sigmoid grad. at point 1:", dx)
x=20
dx = (f(x+e)-f(x))/e
print("sigmoid grad. at point 20:", dx)
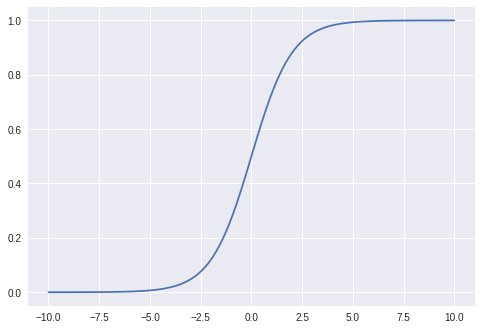
Note we got the following output:
sigmoid at point 1: 0.1965664984852067
sigmoid at point 20: 2.0601298444944405e-09
Look how the second gradient at point x=20 is tiny. Multiplying that number with the similar “small” number would produce what is called the computational instability. In this case vanishing gradient problem.
When ever we work with the sigmoid function, because of this we should take the inputs from range: x>-1, and x<1. This range provides no problems as explained.